


Next: C.2 The eigenvalue equation
Up: C. Proofs
Previous: C. Proofs
C.1 Probabilistic PCA and error measures
In probabilistic principal component analysis, the observed d-dimensional data
{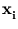 } are assumed to origin from a probability density
p(
} are assumed to origin from a probability density
p(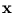 ). This density can be written as
). This density can be written as
p( ) = (2 ) = (2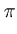 )-d/2(det )-d/2(det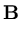 )-1/2exp )-1/2exp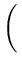 - - 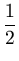 ( ( - - 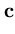 )T )T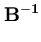 ( ( - - 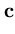 ) ) , , |
(C.1) |
with
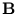 =
= 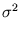
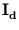 +
+ 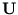
 (Tipping and Bishop, 1997).
(Tipping and Bishop, 1997). 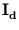 is the d-dimensional identity matrix, and
is the d-dimensional identity matrix, and 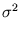 is the noise variance. The d×q matrix
is the noise variance. The d×q matrix 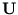 is obtained by maximizing the likelihood of the data
{
is obtained by maximizing the likelihood of the data
{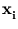 } given the probability
p(
} given the probability
p(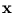 ). Tipping and Bishop (1999) showed that the result is
). Tipping and Bishop (1999) showed that the result is
The columns of the d×q matrix 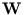 are the q principal
eigenvectors of the covariance matrix of
{
are the q principal
eigenvectors of the covariance matrix of
{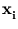 }.
The q largest eigenvalues
}.
The q largest eigenvalues 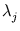 of the covariance matrix are the entries of the diagonal matrix
of the covariance matrix are the entries of the diagonal matrix
 .
. 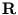 is an arbitrary q×q rotational
matrix.
is an arbitrary q×q rotational
matrix.
In the following, it is shown that the double negative logarithm of (C.1) equals the normalized Mahalanobis distance plus reconstruction error (section 3.2.1) plus a constant. Using (C.2) to rewrite the expression for 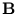 gives
gives
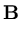 = = 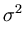 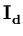 + + 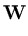 ( (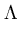 - - 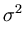 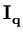 ) )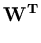 = = 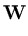 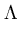 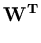 + + 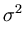 ( (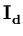 - - 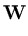 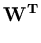 ) . ) . |
(C.3) |
By showing that
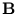
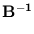 =
= 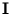 and
and
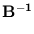
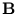 =
= 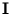 , we can verify that the inverse of
, we can verify that the inverse of 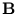 is
is
The eigenvalues of 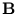 are
are
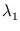 ,...,
,...,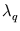 and
and 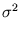 . The latter occurs (d - q)-times. Thus, the determinant of
. The latter occurs (d - q)-times. Thus, the determinant of 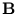 is
is
Finally, we evaluate the logarithm of
p(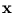 ) using (C.1), (C.4), and (C.5):
) using (C.1), (C.4), and (C.5):
ln p( ) = - ) = -  ln(2 ln(2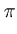 ) - ) - 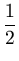 E( E( - - 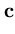 ) ) |
(C.6) |
with
E(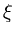 ) = ) = 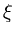 T T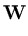 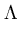 -1 -1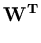 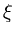 + + 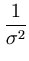 ( (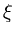 T T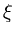 - - 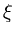 T T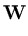 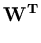 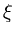 ) + ) + 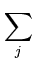 ln ln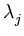 + (d - q)ln + (d - q)ln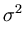 , , |
(C.7) |
and
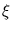 =
= 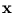 -
-  . E is a normalized Mahalanobis distance plus reconstruction error.
. E is a normalized Mahalanobis distance plus reconstruction error.



Next: C.2 The eigenvalue equation
Up: C. Proofs
Previous: C. Proofs
Heiko Hoffmann
2005-03-22
![]() } are assumed to origin from a probability density
p(
} are assumed to origin from a probability density
p(![]() ). This density can be written as
). This density can be written as
![]() gives
gives
![]() are
are
![]() ,...,
,...,![]() and
and ![]() . The latter occurs (d - q)-times. Thus, the determinant of
. The latter occurs (d - q)-times. Thus, the determinant of ![]() is
is