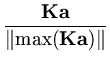


Next: B.2 Kernel PCA speed-up
Up: B. Algorithms
Previous: B. Algorithms
B.1 Power method with deflation
The power method is a common method to extract the eigenvector with the largest eigenvalue (Diamantaras and Kung, 1996). Starting with a random vector 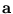 , the principal eigenvector of a matrix
, the principal eigenvector of a matrix 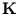 is computed by iterating:
is computed by iterating:
max(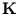
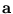 ) is the component of the vector
) is the component of the vector
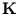
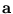 with the largest absolute value (some variants of the power method use
|
with the largest absolute value (some variants of the power method use
|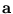 | instead).
This iteration converges to the largest eigenvector with the eigenvalue
| instead).
This iteration converges to the largest eigenvector with the eigenvalue
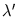 = |max(
= |max(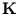
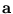 )|. Further eigenvectors are obtained using deflation. After the eigenvector
)|. Further eigenvectors are obtained using deflation. After the eigenvector 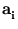 (number i, ordered by the size of the corresponding eigenvalue) is computed, a new matrix
(number i, ordered by the size of the corresponding eigenvalue) is computed, a new matrix
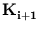 is obtained from the previous one
is obtained from the previous one  by iterating
by iterating
where
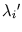 is the eigenvalue corresponding to
is the eigenvalue corresponding to 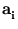 .
.



Next: B.2 Kernel PCA speed-up
Up: B. Algorithms
Previous: B. Algorithms
Heiko Hoffmann
2005-03-22
![]() , the principal eigenvector of a matrix
, the principal eigenvector of a matrix ![]() is computed by iterating:
is computed by iterating: