


Next: 5.3 Experiments
Up: 5.2 Pattern association algorithm
Previous: 5.2.2.1 Examples
5.2.3 Recall
In recall, the components of a pattern 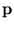 are partially given, and the components of a completed pattern
are partially given, and the components of a completed pattern 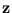 are divided into input and output (see section 4.2). The input is the offset
are divided into input and output (see section 4.2). The input is the offset 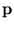 of a hyper-plane extending into the output dimensions:
of a hyper-plane extending into the output dimensions:
where
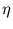 are the free parameters of the hyper-plane. The matrix
are the free parameters of the hyper-plane. The matrix 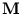 defines which dimensions are input and which are output. To obtain the output for a given input, the free parameters are chosen such that the potential
E(
defines which dimensions are input and which are output. To obtain the output for a given input, the free parameters are chosen such that the potential
E(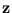 ) is minimized,
) is minimized,
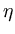 * * |
= |
arg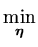 E( E(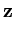 ( (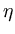 )) , )) , |
|
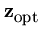 |
= |
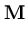 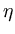 * + * + 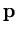 . . |
(5.11) |
There seems to be no analytical solution for
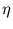 *. In feature space, the constraint space is not a hyper-plane. However, the minimization can be solved using standard numerical optimization algorithms.
*. In feature space, the constraint space is not a hyper-plane. However, the minimization can be solved using standard numerical optimization algorithms.



Next: 5.3 Experiments
Up: 5.2 Pattern association algorithm
Previous: 5.2.2.1 Examples
Heiko Hoffmann
2005-03-22
![]() are partially given, and the components of a completed pattern
are partially given, and the components of a completed pattern ![]() are divided into input and output (see section 4.2). The input is the offset
are divided into input and output (see section 4.2). The input is the offset ![]() of a hyper-plane extending into the output dimensions:
of a hyper-plane extending into the output dimensions: