HOME
Kernel PCA for novelty detection
This website accompanies the article "Kernel PCA for Novelty Detection" (Pattern Recognition, 2007). The site provides matlab-code of the algorithm and the two-dimensional point distributions used in the article. Please, cite this article if you use any of the material presented here for any publication.
Matlab code demonstrating the algorithm
In kernel PCA for novelty detection, the reconstruction error in feature space is used as a measure for novelty. The following matlab code demonstrates the reconstruction error for a given 2-D point distribution and shows the resulting decision boundary enclosing all data points.
Download code:
Download and unzip the file kpca.zip [8 KB].
The zip archive contains three m-files: kpcabound.m, recerr.m, and kernel.m. The last two are helper functions for the demo program kpcabound. kpcabound has as input the data set, the kernel parameter (here, sigma of a Gaussian function), the number of eigenvectors to be extracted, and the number of points outside the decision boundary.
Test code:
For the following test, you need the file ring-line-square.dat from the data-distribution archive below. In matlab, type
A = load('ring-line-square.dat');
kpcabound(A,0.4,40,0)
These commands should result in the following figure:
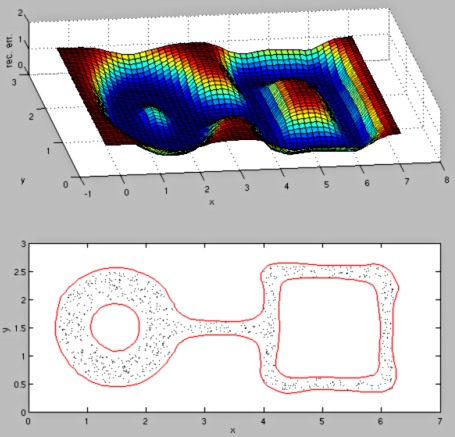
If you look closely at the resulting decision boundaries, you may find a small difference from the curves published in the article. This difference results from the coarser grid used in the matlab code to compute the reconstruction-error surface (the grid is coarser to increase computation speed).
Two-dimensional synthetic distributions
The following archive contains five distributions: square, square-noise, ring-line-square, spiral, and sine-noise. Their generation is described in the above mentioned article.
Attributes: Two columns contain the (x,y)-coordinates of each data point.
Download: testdist.zip [28 KB]
Install: type unzip testdist.zip (in Windows use, e.g., Winzip or GnuWin UnZip)
Unzipping will extract five files: square.dat, square-noise.dat, ring-line-square.dat, spiral.dat, and sine-noise.dat.
15 Apr 2007