The computational load for the projection onto a principal component is high, n evaluations of
k(![]() ,
,![]() ). In the context of support vector machines, Burges (1996) introduced a speed-up usable for the extraction of the principal components (Schölkopf et al. (1998b) suggested that this could be also used for kernel PCA). The idea is to approximate each vector
). In the context of support vector machines, Burges (1996) introduced a speed-up usable for the extraction of the principal components (Schölkopf et al. (1998b) suggested that this could be also used for kernel PCA). The idea is to approximate each vector
![]() =
= ![]()
![]()
![]() (
(![]() ) by another vector
) by another vector ![]() using only a small set of vectors
using only a small set of vectors ![]() from the original space, instead of the whole set
{
from the original space, instead of the whole set
{![]() },
},
Here, instead of minimizing
||![]() -
- ![]() ||2 to determine the reduced set, we use a method introduced by Schölkopf et al. (1998a). It is computationally expensive to optimize over the whole reduced set simultaneously; thus instead, an iterative method extracts the
||2 to determine the reduced set, we use a method introduced by Schölkopf et al. (1998a). It is computationally expensive to optimize over the whole reduced set simultaneously; thus instead, an iterative method extracts the ![]() one by one. Moreover, the optimization over
one by one. Moreover, the optimization over ![]() and
and ![]() is split.
is split.
First, starting with ![]() , we minimize the distance between
, we minimize the distance between ![]() and its projection onto the span of
and its projection onto the span of
![]() (
(![]() ),
),
After ![]() is determined, the optimal
is determined, the optimal ![]() is computed. Generally, if the values
is computed. Generally, if the values ![]() are known, the corresponding optimal
are known, the corresponding optimal ![]() can be obtained analytically by setting the derivatives
can be obtained analytically by setting the derivatives
![]() ||
||![]() -
- ![]() ||2 zero (Schölkopf et al., 1998a). The result is
||2 zero (Schölkopf et al., 1998a). The result is
![]()
![]() (
(![]() ) alone is not enough to replace w. Therefore, the second point
) alone is not enough to replace w. Therefore, the second point ![]() is chosen such that the remaining vector
is chosen such that the remaining vector
![]() -
- ![]()
![]() (
(![]() ) is approximated by
) is approximated by
![]()
![]() (
(![]() ). This leads to an iterative scheme, with
). This leads to an iterative scheme, with
![]() =
= ![]() -
- ![]()
![]() (
(![]() ), starting with
), starting with
![]() =
= ![]() . At each step,
. At each step, ![]() is approximated by
is approximated by
![]()
![]() (
(![]() ). That is,
). That is, ![]() is obtained by maximizing (B.5), and then,
{
is obtained by maximizing (B.5), and then,
{![]() | i = 1,..., t} are calculated using (B.6). Every iteration step, every addition of a set
(
| i = 1,..., t} are calculated using (B.6). Every iteration step, every addition of a set
(![]() ,
,![]() ), reduces the distance to the vector
), reduces the distance to the vector ![]() . In this way, the complete reduced set can be obtained.
. In this way, the complete reduced set can be obtained.
In kernel PCA, more than one vector needs to be approximated. To do this, the above method can be generalized (Schölkopf et al., 1998a). Instead of (B.4), the sum of the square projection distances is minimized,
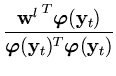 |
(B.7) |
The result of this reduced set method is that all vectors that are expressed as a sum over n kernel functions, can be obtained as a sum over only m kernel functions. Thus, the speed gain is n/m.