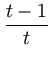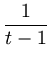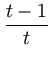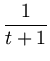


Next: B. Algorithms
Up: A. Statistical tools
Previous: A.2 Maximum likelihood
A.3 Iterative mean
The mean value of a distribution {xi} can also be computed iteratively if the values xi are drawn one-by-one. Let
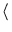 x
x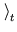 be the average over the first t data points. We observe that
be the average over the first t data points. We observe that
 x x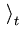 |
= |
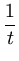 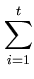 xi xi |
|
| |
= |
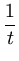 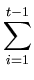 xi + xi + 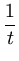 xt xt |
|
| |
= |
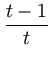 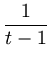 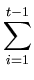 xi + xi + 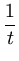 xt xt |
|
| |
= |
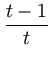 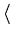 x x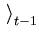 + + 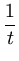 xt . xt . |
(A.13) |
Thus, the update rule for the temporary mean
c(t + 1) = 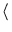 x
x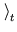 upon presentation of a value x is
upon presentation of a value x is
c(t + 1) = c(t) + 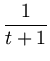  x - c(t) x - c(t) . . |
(A.14) |
This rule is the same as for the center update in vector quantization with a learning rate that decays as 1/t.



Next: B. Algorithms
Up: A. Statistical tools
Previous: A.2 Maximum likelihood
Heiko Hoffmann
2005-03-22
![]() x
x![]() be the average over the first t data points. We observe that
be the average over the first t data points. We observe that