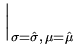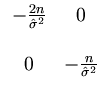


Next: A.3 Iterative mean
Up: A. Statistical tools
Previous: A.1 Bayes' theorem
A.2 Maximum likelihood
The maximum likelihood principle is illustrated in an example with a one-dimensional data distribution {xi},
i = 1,..., n. We assume that the data originate from a Gaussian distribution p(x) with parameters  and
and 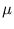 ,
,
According to the maximum likelihood principle,
we will choose the unknown parameters such that the given data are most likely under the obtained distribution. The probability L of the given data set is
L(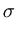 , ,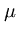 ) = ) =  p(xi) = p(xi) = 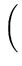 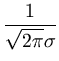 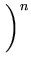 exp exp - -  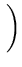 . . |
(A.4) |
We want to find
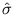 and
and 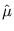 that maximize L. Maximizing L is equivalent to maximizing log L, which is also called the log-likelihood
that maximize L. Maximizing L is equivalent to maximizing log L, which is also called the log-likelihood
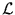 ,
,
 ( (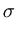 , ,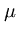 ) = log L( ) = log L(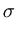 , ,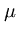 ) = - n log ) = - n log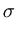 - -  + const . + const . |
(A.5) |
To find the maximum we compute the derivatives of the log-likelihood
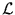 and set them to zero:
and set them to zero:
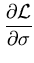 |
= |
- 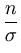 + + 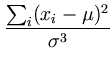  0 , 0 , |
(A.6) |
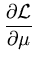 |
= |
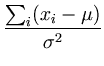 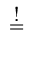 0 . 0 . |
(A.7) |
Thus, we obtain the values of the parameters
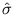 and
and 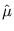 :
:
The resulting
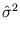 is the variance of the distribution and
is the variance of the distribution and 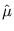 is its center. The extremum of
is its center. The extremum of
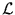 is indeed a local maximum, as can be seen by computing the Hesse matrix of
is indeed a local maximum, as can be seen by computing the Hesse matrix of
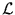 and evaluating it at the extreme point
(
and evaluating it at the extreme point
(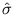 ,
,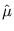 ):
):
 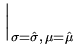 |
= |
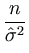 - - 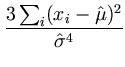 = = 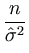 - - 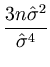 = - = -  , , |
(A.11) |
| |
|
|
|
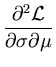 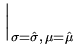 |
= |
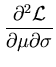 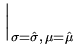 = - = - 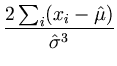 = 0 , = 0 , |
|
| |
|
|
|
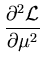 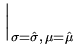 |
= |
- 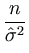 . . |
|
It follows that the Hesse matrix at the extremum is negative definite,
Therefore, the extremum is a local maximum. Moreover, it is also a global maximum. First, for finite parameters, no other extrema exist because
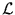 is a smooth function. Second,
is a smooth function. Second,
 is positive for finite parameters, but approaches zero for infinite values. Thus, any maximum must be in the finite range.
is positive for finite parameters, but approaches zero for infinite values. Thus, any maximum must be in the finite range.

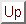


Next: A.3 Iterative mean
Up: A. Statistical tools
Previous: A.1 Bayes' theorem
Heiko Hoffmann
2005-03-22
![]() and
and ![]() ,
,
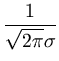 exp
exp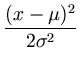
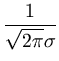

 + const .
+ const .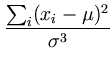
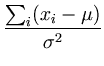
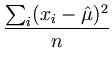 ,
,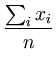 .
.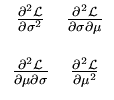
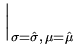
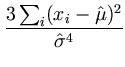 =
= 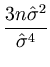 = -
= - 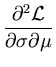
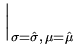
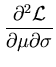
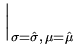 = -
= - 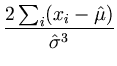 = 0 ,
= 0 ,