To learn sensorimotor relations, Ritter et al. (1990) used the self-organizing map (SOM) algorithm (Kohonen, 1995).
This algorithm fits a q-dimensional grid to a distribution of training patterns in
IRd, q![]() d (Kohonen, 1982). SOMs were motivated by sensory maps in the brain, for example, the somatosensory map or the tonotopic map (Kohonen, 1989). A SOM consists of a q-dimensional array1.8 of nodes; each node i has a location
d (Kohonen, 1982). SOMs were motivated by sensory maps in the brain, for example, the somatosensory map or the tonotopic map (Kohonen, 1989). A SOM consists of a q-dimensional array1.8 of nodes; each node i has a location ![]() and a weight vector
and a weight vector ![]() (figure 1.7). The weight vectors are in the space of the training patterns.
(figure 1.7). The weight vectors are in the space of the training patterns.
![\includegraphics[width=15cm]{som.eps}](img48.gif)
|
The algorithm consists of three steps, which are alternated until convergence is reached. First, a training pattern ![]() is drawn randomly. Second, the node c is determined whose weight vector
is drawn randomly. Second, the node c is determined whose weight vector ![]() is closest to
is closest to ![]() ,
,
hic = 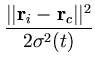 |
(1.4) |
The SOM algorithm can be easily extended by adding more parameters to each node and by updating them in parallel to the weight vectors. With such an extension, Ritter and Schulten (1986) used the SOM to learn sensorimotor relations. Here, a training pattern consists of a pair (![]() ,y) of sensor values
,y) of sensor values ![]() and corresponding motor values
and corresponding motor values ![]() . Such a sensorimotor pattern is an element in the space formed by the Cartesian product of the sensor and the motor space. The SOM extension has two weight vectors for each node i, one for the sensory input,
. Such a sensorimotor pattern is an element in the space formed by the Cartesian product of the sensor and the motor space. The SOM extension has two weight vectors for each node i, one for the sensory input,
![]() , and one for the motor output,
, and one for the motor output,
![]() . The computation (1.2) of the best matching node is restricted to the sensory domain; but both
. The computation (1.2) of the best matching node is restricted to the sensory domain; but both
![]() and
and
![]() are updated according to (1.3) (
are updated according to (1.3) (
![]() is updated based on
is updated based on ![]() , and the neighborhood function may have different parameters).
, and the neighborhood function may have different parameters).
This algorithm fits the grid of weight vectors
(![]() ,
,![]() ) to the sensorimotor pattern distribution. The resulting link between a sensory input
) to the sensorimotor pattern distribution. The resulting link between a sensory input
![]() and a motor output
and a motor output
![]() provides a discrete mapping, usable for an inverse model. To obtain a continuous mapping, Ritter et al. (1989) further added a locally linear map to each node. The result was successfully applied to control a robot arm with three degrees of freedom.
provides a discrete mapping, usable for an inverse model. To obtain a continuous mapping, Ritter et al. (1989) further added a locally linear map to each node. The result was successfully applied to control a robot arm with three degrees of freedom.
![\includegraphics[width=12cm]{one-to-manySOM.eps}](img61.gif)
|
The restriction of the node competition (1.2) to the distance in sensory space reduces the search space for the weights, but it makes the approach fail on one-to-many mappings (figure 1.8). The learning for
![]() is independent of
is independent of
![]() . As a result, a classical SOM algorithm is applied solely to the sensory domain, while
. As a result, a classical SOM algorithm is applied solely to the sensory domain, while
![]() is updated simultaneously. In the case of two possible target values for one sensory input,
is updated simultaneously. In the case of two possible target values for one sensory input,
![]() is attracted to two different positions
is attracted to two different positions ![]() and
and ![]() (because the node competition is independent of the distance to
(because the node competition is independent of the distance to ![]() or
or ![]() ). Thus, as a result from the update rule (1.3),
). Thus, as a result from the update rule (1.3),
![]() will be averaged among
will be averaged among ![]() and
and ![]() . For example, given that both
. For example, given that both ![]() and
and ![]() are drawn with the same probability (p = 0.5), on average,
are drawn with the same probability (p = 0.5), on average,
![]() is updated according to
is updated according to
| = | |||
| = | (1.5) |
Further limitations arise from the SOM grid structure. First, since sensorimotor manifolds are usually non-linear, many grid points are needed. With increasing dimensionality q of the manifold, the number of necessary points increases exponentially (the number of points per dimension to the power of q). Soon (q > 3), this gets computationally unfeasible. As a solution to this problem, Martinetz and Schulten (1990) suggested an extension to hierarchical SOM. A second limitation arises in real world applications: some sensor values could be pure noise (or irrelevant to the sensorimotor map). Such noise dimensions need to be filled with grid points (figure 1.9), resulting in the same problems as mentioned above.
![\includegraphics[width=9cm]{noisedim.eps}](img75.gif)
|