4.4.1.2 Results

All training methods of the abstract RNN had similar errors and showed about the same performance than an MLP (table 4.1). NGPCA was slightly better than NGPCA-constV and the single unit (all other comparisons did not show a significant difference).

Table 4.1: Average square error per pixel (SE) for each training method. The standard error for all mean values was around 0.0001.

training method	SE
NGPCA	0.0036
NGPCA-constV	0.0039
MPPCA-ext	0.0037
single unit (q = 100)	0.0039
single unit (q = 50)	0.0042
MLP	0.0037

The remaining results were gained by using NGPCA for training. On individual image windows, the abstract RNN could complete structures like edges and uniform surfaces, but isolated structures in the center square could not be foreseen (figure 4.5). The two test images with 850 holes could be completed to almost the quality of the original images (figure 4.7). However, tilted edges and the details of leaves could not be completed correctly.

The MLP can learn only one recall direction (at once). However, for the abstract RNN, arbitrary pixels can be chosen as input (figure 4.6).

Figure 4.5: Four randomly chosen recall examples. In each pair of images, the left one shows the original image, and the right one presents the recall result. The square encloses the pixels marked as output.

Figure 4.6: Mean square error per pixel (SE) for different output windows. For A, B, D, and E the standard error was about 0.0001, and 0.0002 for C.

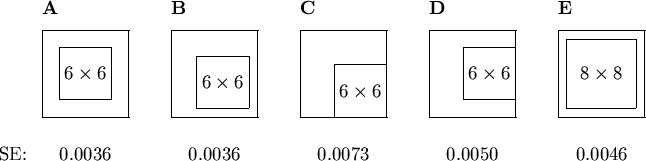Figure 4.7: In each block of four pictures, the top left shows the test image with 850 holes, the top right shows the restored image using the abstract RNN, the bottom left shows the restored image using the average color (see text), and the bottom right shows the absolute difference between the RNN restored image and the original test image (white = 0, black = 1).