


Next: 4.7 Discussion
Up: 4. Abstract recurrent neural
Previous: 4.5.2 Results
4.6 Dependence on the number of input dimensions
As shown in section 4.5, the performance of the abstract recurrent neural network depends on the number of input dimensions chosen. A higher number of input dimensions results in a higher sum of square errors per pattern. This relationship is investigated theoretically on a simplified abstract RNN.
The first simplification is that the model consists of spheres instead of ellipsoids. Thus, the distribution of training data is approximated by a set of m code-book vectors 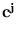 , and for each of them the potential field is given by the Euclidean distance. The second simplification is that the code-book vectors are uniformly randomly distributed. This is justified for distributions that are wrapped inside the pattern space, and are not restricted to embedded hyper-planes, as it is likely the case for the kinematic arm model. Recall works as in section 4.2 (see also figure 4.14).
, and for each of them the potential field is given by the Euclidean distance. The second simplification is that the code-book vectors are uniformly randomly distributed. This is justified for distributions that are wrapped inside the pattern space, and are not restricted to embedded hyper-planes, as it is likely the case for the kinematic arm model. Recall works as in section 4.2 (see also figure 4.14).
Figure 4.14:
The trained abstract network consists of a set of code-book vectors, here illustrated as circles. These vectors are distributed randomly. Recall happens by finding the closest vector to a constraint space (gray line). The
offset of this line from the origin is the input.
|
|
We assume that the code-book vectors lie inside a d-dimensional cube of side length two, centered at the origin. Since the code-book vectors are
distributed uniformly, the average error is independent of the specific value of the input (offset of the constrained space)4.3. Thus, we arrange the constrained spaces such that they all go through the
origin. If d - 1 input dimensions are given, the constraint is the
xd-axis. For d - 2 input dimensions the axis xd and xd-1 span the
constraint space, and so on (see figure 4.15 as an
example). Instead of choosing different input values to compute the sum of
square errors, we draw a new set of 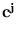 from a random distribution
for each test trial.
from a random distribution
for each test trial.
Figure 4.15:
Example using r = 1 input dimensions in a n = 3 dimensional
space. The x2x3 plane is the constrained space. Code-book vectors are
illustrated as circles. Possible code-book locations are enclosed by the cube drawn with dotted lines. The dashed lines show the distances between constraint and code-book vectors.
|
|
Given r input dimensions, the squared distance Ej of 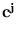 to the
constrained space is
to the
constrained space is
We define the square error E as the minimum squared distance to the data approximation (in the kinematic arm model, this matches the computation of the square error in the case of arbitrary directions, see section 4.5.1). Thus,
E = min 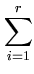 (c1i)2, (c1i)2,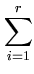 (c2i)2,..., (c2i)2,...,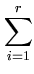 (cmi)2 (cmi)2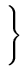 . . |
(4.9) |
The sum of square errors per pattern is the expectation value of E given a
random distribution of 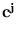 . To compute the expectation of a minimum, we use the
following trick (Wentzell, 2003). The cumulative probability Pc(T) that all Ej are larger than a threshold T is computed. Pc(T) is monotone descending, starting with Pc(0) = 1. The negative derivative of Pc(T) can be interpreted as the probability density function of T. For a given T, this function provides the probability density that T equals the smallest member of the set {Ej}. Thus, the expectation value of T (the first momentum of the probability density function) equals the expectation value of E, the minimum of {Ej}. Therefore,
. To compute the expectation of a minimum, we use the
following trick (Wentzell, 2003). The cumulative probability Pc(T) that all Ej are larger than a threshold T is computed. Pc(T) is monotone descending, starting with Pc(0) = 1. The negative derivative of Pc(T) can be interpreted as the probability density function of T. For a given T, this function provides the probability density that T equals the smallest member of the set {Ej}. Thus, the expectation value of T (the first momentum of the probability density function) equals the expectation value of E, the minimum of {Ej}. Therefore,
The probability p that a point 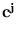 has a squared distance
Ej larger or equal to T is the cube volume outside the r-sphere4.4with radius
has a squared distance
Ej larger or equal to T is the cube volume outside the r-sphere4.4with radius 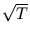 centered at the origin divided by the cube volume (figure 4.16). The cumulative probability Pc is p to the power of m.
centered at the origin divided by the cube volume (figure 4.16). The cumulative probability Pc is p to the power of m.
Figure 4.16:
The gray area relative to the total area of the square is the
probability that a point lies outside the circle. Two examples with different radii are shown.
|
|
To make the function p over T analytically integrable, we make an approximation. The r-cube, the space of all possible codebook vectors (in
the first r dimensions), is replaced by an r-sphere with radius 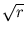 centered at the origin. This sphere encloses tightly the r-cube. To
compensate this step, we multiply the number of codebook vectors m with the
r-sphere volume divided by the r-cube volume. The volume of an r-sphere
with unit radius can be written as
centered at the origin. This sphere encloses tightly the r-cube. To
compensate this step, we multiply the number of codebook vectors m with the
r-sphere volume divided by the r-cube volume. The volume of an r-sphere
with unit radius can be written as
Vr = 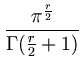 . . |
(4.11) |
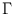 is the Gamma-function. It is related to the factorial by
is the Gamma-function. It is related to the factorial by
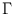 (n) = (n - 1)! for positive integers n. For r = 2, for example, the above volume Vr equals
(n) = (n - 1)! for positive integers n. For r = 2, for example, the above volume Vr equals 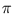 . Hence, the resulting volume relation vr (here, for the sphere radius
. Hence, the resulting volume relation vr (here, for the sphere radius 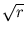 ) is
) is
vr = 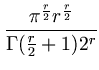 . . |
(4.12) |
The above step is justified by the uniform distribution of the
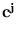 . But, it is not an equivalence transformation (for r > 1). The quality of this approximation will be tested later. The resulting number of
vectors,
. But, it is not an equivalence transformation (for r > 1). The quality of this approximation will be tested later. The resulting number of
vectors,
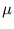 = int(vrm), is rounded to an integer value. With the approximation, the
probability p(T) that a vector has a squared distance Ej
= int(vrm), is rounded to an integer value. With the approximation, the
probability p(T) that a vector has a squared distance Ej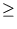 T can be expressed as
T can be expressed as
p(T) = 1 - 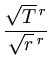 . . |
(4.13) |
The total probability Pc that all vectors fulfill the above condition is
Pc(T) = 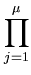 p(T) = (1 - ( p(T) = (1 - (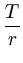 ) )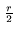 ) )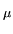 . . |
(4.14) |
The value of T extends from 0 to r. Using (4.10), we obtain for
the expectation value of E
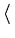 E E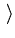 = - = - 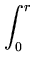 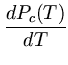 T dT = T dT = 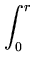 Pc(T)dT - Pc(T)T Pc(T)dT - Pc(T)T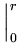 = = 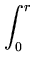 Pc(T)dT . Pc(T)dT . |
(4.15) |
The second equality sign uses integration by parts, the last equality sign
uses (4.14). The final integration, using (4.14), gives
The integral was solved with the help of
MATLAB® and its symbolic toolbox. Using the equality
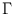 (x) = (x - 1)
(x) = (x - 1)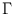 (x - 1), the expression can be simplified to
(x - 1), the expression can be simplified to
For large 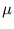 , the latter is more feasible for numerical evaluation than (4.16).
We further investigate the quality of our approximation. The case m = 1 can be evaluated correctly. For one codebook vector, the expectation of its
squared distance can be directly calculated:
, the latter is more feasible for numerical evaluation than (4.16).
We further investigate the quality of our approximation. The case m = 1 can be evaluated correctly. For one codebook vector, the expectation of its
squared distance can be directly calculated:
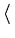 E E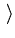 = 2-r = 2-r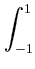 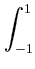 ... ... 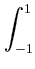 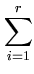 ci2 ci2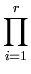 dci = 2-rr dci = 2-rr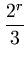 = = 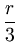 . . |
(4.18) |
Figure 4.17 shows the result of this comparison. The mismatch
increases with the number of input dimensions r.
Figure 4.17:
Comparison between the approximation, replacing the r-cube by a r-sphere resulting in (4.12) and (4.17), and the correctly evaluated result (4.18) for one code-book vector.
|
|
We want to check our approximation using larger m. The result from (4.12) and (4.17) was compared to a simulation, in which 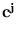 were drawn randomly from a r-cube with side length 2. Figure 4.18 shows the result, using r = 10 input dimensions and 100 000 trials for each m value in the simulation. The approximation got better the more codebook vectors were used. The number of codebook vectors needed for a good approximation depends on the value of r. The higher r, the more vectors are needed.
were drawn randomly from a r-cube with side length 2. Figure 4.18 shows the result, using r = 10 input dimensions and 100 000 trials for each m value in the simulation. The approximation got better the more codebook vectors were used. The number of codebook vectors needed for a good approximation depends on the value of r. The higher r, the more vectors are needed.
Figure 4.18:
Comparison between the theory, using (4.12) and
(4.17), and the result from a simulation, with r = 10. The number of code-book vectors is m.
|
|
Finally, the dependency on the number of input dimensions is demonstrated for the case m = 200. As above, the
theory is compared to a simulation, using 100 000 trials for each r
value. In this test, theory and simulation results did overlap (figure 4.19). Between r = 5 and r = 8 the increase is approximately exponential with exponent 0.69.
Figure 4.19:
Dependency of the mean square error per output dimension on the number of input dimensions r for m = 200 (d = 10). Theory, using (4.12) and (4.17), and simulation
results are shown.
|
|



Next: 4.7 Discussion
Up: 4. Abstract recurrent neural
Previous: 4.5.2 Results
Heiko Hoffmann
2005-03-22
![]() , and for each of them the potential field is given by the Euclidean distance. The second simplification is that the code-book vectors are uniformly randomly distributed. This is justified for distributions that are wrapped inside the pattern space, and are not restricted to embedded hyper-planes, as it is likely the case for the kinematic arm model. Recall works as in section 4.2 (see also figure 4.14).
, and for each of them the potential field is given by the Euclidean distance. The second simplification is that the code-book vectors are uniformly randomly distributed. This is justified for distributions that are wrapped inside the pattern space, and are not restricted to embedded hyper-planes, as it is likely the case for the kinematic arm model. Recall works as in section 4.2 (see also figure 4.14).
![\includegraphics[width=9cm]{network.eps}](img325.gif)
![]() from a random distribution
for each test trial.
from a random distribution
for each test trial.
![\includegraphics[width=9cm]{constraint.eps}](img326.gif)
![]() to the
constrained space is
to the
constrained space is
![\includegraphics[width=13cm]{probarea.eps}](img339.gif)
![]() centered at the origin. This sphere encloses tightly the r-cube. To
compensate this step, we multiply the number of codebook vectors m with the
r-sphere volume divided by the r-cube volume. The volume of an r-sphere
with unit radius can be written as
centered at the origin. This sphere encloses tightly the r-cube. To
compensate this step, we multiply the number of codebook vectors m with the
r-sphere volume divided by the r-cube volume. The volume of an r-sphere
with unit radius can be written as
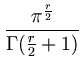 .
.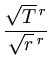 .
.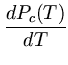 T dT =
T dT = ![\includegraphics[width=11.3cm]{dependinput/checkm1.eps}](img359.gif)
![]() were drawn randomly from a r-cube with side length 2. Figure 4.18 shows the result, using r = 10 input dimensions and 100 000 trials for each m value in the simulation. The approximation got better the more codebook vectors were used. The number of codebook vectors needed for a good approximation depends on the value of r. The higher r, the more vectors are needed.
were drawn randomly from a r-cube with side length 2. Figure 4.18 shows the result, using r = 10 input dimensions and 100 000 trials for each m value in the simulation. The approximation got better the more codebook vectors were used. The number of codebook vectors needed for a good approximation depends on the value of r. The higher r, the more vectors are needed.
![\includegraphics[width=11.7cm]{dependinput/checkr10.eps}](img360.gif)
![\includegraphics[width=12cm]{dependinput/inputdim.eps}](img361.gif)