


Next: 5.2.2.1 Examples
Up: 5.2 Pattern association algorithm
Previous: 5.2.1 Spherical potential
5.2.2 Cylindrical potential
We use the reconstruction error (Diamantaras and Kung, 1996, p. 45) as a potential field in feature space,
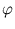 is a vector originating in the center of the distribution in feature space,
is a vector originating in the center of the distribution in feature space,
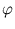 (
(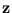 ) =
) = 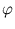 (
(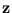 ) -
) - 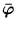 . The matrix
. The matrix 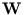 contains the q row vectors
contains the q row vectors
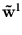 (q is the number of principal components)5.2.
(q is the number of principal components)5.2.
We need to eliminate
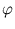 in (5.5), and write the potential as a function of a vector
in (5.5), and write the potential as a function of a vector 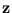 taken from the original space. The projection
fl(
taken from the original space. The projection
fl(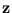 ) of
) of
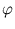 (
(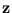 ) onto the eigenvectors
) onto the eigenvectors
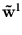 =
= 
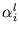
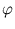 (
(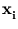 ) can be readily evaluated using the kernel function k,
) can be readily evaluated using the kernel function k,
fl(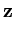 ) ) |
= |
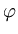 ( (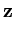 )T )T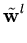 |
|
| |
= |
 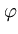 ( (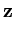 ) - ) - 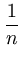 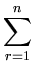 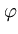 ( (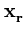 ) )![$\displaystyle \left.\vphantom{\boldsymbol{\varphi}({\bf z})-\frac{1}{n}\sum_{r=1}^n \boldsymbol{\varphi}({\bf x}_r)}\right]^{T}_{}$](img382.gif)  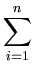 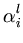 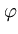 ( (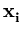 ) - ) - 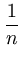 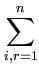 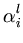 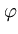 ( (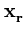 ) )![$\displaystyle \left.\vphantom{\sum_{i=1}^n\alpha_i^l\boldsymbol{\varphi}({\bf x}_i)-\frac{1}{n}\sum_{i,r=1}^n \alpha_i^l\boldsymbol{\varphi}({\bf x}_r)}\right]$](img386.gif) |
|
| |
= |
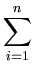 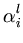  k( k(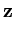 , ,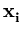 ) - ) - 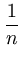 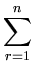 k( k(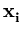 , ,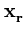 ) - ) - 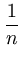 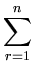 k( k(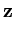 , ,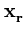 ) ) |
|
| |
+ |
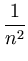 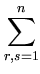 k( k(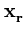 , ,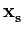 ) )![$\displaystyle \Bigg]$](img389.gif) . . |
(5.6) |
The second equality uses (5.1). As a result,
E(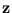 ) can be expressed as
) can be expressed as
The scalar product
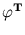
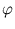 equals the potential field of a sphere (5.3). Thus, the expression of the potential
E(
equals the potential field of a sphere (5.3). Thus, the expression of the potential
E(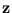 ) can be further simplified to
) can be further simplified to
E(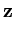 ) = ES( ) = ES(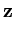 ) - ) - 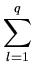 fl( fl(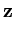 )2 , )2 , |
(5.8) |
which is the desired form of the cylindrical potential.
The above computation of
fl(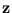 ) requires n evaluations of the kernel function for each
) requires n evaluations of the kernel function for each 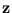 . Since, for each component l, the same kernel can be used, the total number of kernel evaluations is also n. With the speed-up described in appendix B.2, this number can be reduced to m. Here, the expression
. Since, for each component l, the same kernel can be used, the total number of kernel evaluations is also n. With the speed-up described in appendix B.2, this number can be reduced to m. Here, the expression

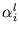
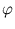 (
(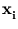 ) is estimated by
) is estimated by
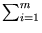
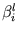
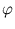 (
(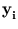 ), and
1/n
), and
1/n
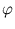 (
(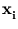 ) by
) by
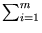
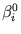
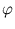 (
(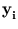 ). Doing these replacements, the equation for
fl(
). Doing these replacements, the equation for
fl(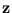 ) (5.6) can be approximated by
) (5.6) can be approximated by
fl(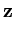 ) ) |
= |
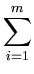 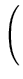 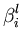 - - 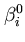 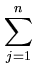 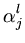  k( k(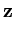 , ,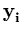 ) ) |
|
| |
- |
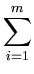 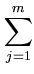 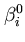  k( k(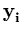 , ,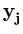 ) + ) + 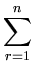 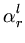 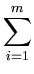 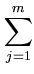 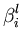  k( k(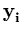 , ,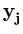 ) . ) . |
(5.9) |
The last two terms and
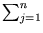
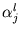 do not need to be evaluated for each
do not need to be evaluated for each 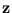 , but can be computed beforehand. Therefore, the computation is dominated by the m evaluations of the kernel function, which need to be carried out only once for all eigenvectors l.
, but can be computed beforehand. Therefore, the computation is dominated by the m evaluations of the kernel function, which need to be carried out only once for all eigenvectors l.
Subsections



Next: 5.2.2.1 Examples
Up: 5.2 Pattern association algorithm
Previous: 5.2.1 Spherical potential
Heiko Hoffmann
2005-03-22
![]() in (5.5), and write the potential as a function of a vector
in (5.5), and write the potential as a function of a vector ![]() taken from the original space. The projection
fl(
taken from the original space. The projection
fl(![]() ) of
) of
![]() (
(![]() ) onto the eigenvectors
) onto the eigenvectors
![]() =
= ![]()
![]()
![]() (
(![]() ) can be readily evaluated using the kernel function k,
) can be readily evaluated using the kernel function k,
![]() ) requires n evaluations of the kernel function for each
) requires n evaluations of the kernel function for each ![]() . Since, for each component l, the same kernel can be used, the total number of kernel evaluations is also n. With the speed-up described in appendix B.2, this number can be reduced to m. Here, the expression
. Since, for each component l, the same kernel can be used, the total number of kernel evaluations is also n. With the speed-up described in appendix B.2, this number can be reduced to m. Here, the expression
![]()
![]()
![]() (
(![]() ) is estimated by
) is estimated by
![]()
![]()
![]() (
(![]() ), and
1/n
), and
1/n![]()
![]() (
(![]() ) by
) by
![]()
![]()
![]() (
(![]() ). Doing these replacements, the equation for
fl(
). Doing these replacements, the equation for
fl(![]() ) (5.6) can be approximated by
) (5.6) can be approximated by