


Next: A.2 Maximum likelihood
Up: A. Statistical tools
Previous: A. Statistical tools
A.1 Bayes' theorem
The probability
p(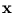 , j) of observing both
, j) of observing both 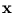 and j can be written in two ways,
and j can be written in two ways,
p( , j) = p( , j) = p( | j)P(j) = P(j| | j)P(j) = P(j| )p( )p( ) . ) . |
(A.1) |
p(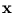 ) is the probability of
) is the probability of 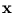 (independent of j), P(j) is the probability of j (independent of
(independent of j), P(j) is the probability of j (independent of 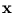 ),
p(
),
p(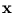 | j) is the probability of
| j) is the probability of 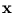 under the condition that j is given, and
P(j|
under the condition that j is given, and
P(j|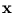 ) is the probability of j under the condition that
) is the probability of j under the condition that 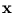 is given. Reorganizing (A.1) about
P(j|
is given. Reorganizing (A.1) about
P(j|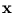 ) gives
) gives
P(j| ) = ) = 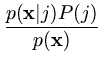 . . |
(A.2) |
This is Bayes' theorem.
Heiko Hoffmann
2005-03-22
![]() , j) of observing both
, j) of observing both ![]() and j can be written in two ways,
and j can be written in two ways,
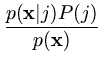 .
.