


Next: 3.2.3 Simulations
Up: 3.2 Extension of Neural
Previous: 3.2.1 Algorithm
3.2.2 Alternative distance measure
For some applications, it proved to be of advantage to modify the error measure
E(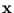 ). The error (3.2) depends on the size of the hyper-ellipsoid. Its volume is proportional to
V =
). The error (3.2) depends on the size of the hyper-ellipsoid. Its volume is proportional to
V = 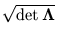
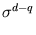 . For a big ellipsoid, (3.2) has therefore a huge bias, namely 2 ln V. Thus, if the other ellipsoids are much smaller, this huge ellipsoid often has a high rank, independent of the Euclidean distance of
. For a big ellipsoid, (3.2) has therefore a huge bias, namely 2 ln V. Thus, if the other ellipsoids are much smaller, this huge ellipsoid often has a high rank, independent of the Euclidean distance of 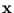 to the center of the ellipsoid. Since the weight
to the center of the ellipsoid. Since the weight 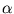 decreases exponentially with the rank,
decreases exponentially with the rank, 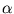 is almost zero, and the ellipsoid cannot change its size anymore, it is `dead' (for example, figure 3.8.A). Thus, to avoid dead units, we tested an alternative error measure that is independent of the volume of the ellipsoid. This can be achieved by normalizing
is almost zero, and the ellipsoid cannot change its size anymore, it is `dead' (for example, figure 3.8.A). Thus, to avoid dead units, we tested an alternative error measure that is independent of the volume of the ellipsoid. This can be achieved by normalizing 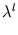 and
and 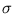 such that the resulting volume
such that the resulting volume 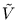 is one. Let
is one. Let
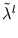 and
and
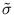 be the normalized values. They can be computed by
be the normalized values. They can be computed by
Using these substitutions, it can be straight-forwardly verified that the new volume
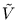 =
= 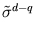
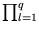
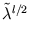 fulfills
fulfills
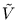 = 1. To compute the modified error, we replace
= 1. To compute the modified error, we replace 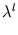 and
and 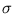 by their normalized values, and then we use the substitution (3.9) to obtain the error again in the original variables,
by their normalized values, and then we use the substitution (3.9) to obtain the error again in the original variables,
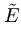 ( (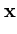 ) = ) = 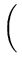 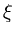 T T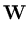 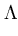 -1 -1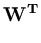 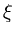 + + 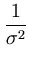 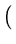 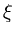 T T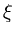 - - 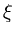 T T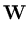 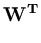 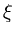  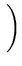 V2/d . V2/d . |
(3.10) |
Here, the logarithm terms can be omitted because they are the same for all units. The modified algorithm uses (3.10) instead of (3.2) for the competition of the units. Everything else stays unchanged. The ellipsoids are still allowed to change their size according to the local PCA. In the following, this algorithm will be called `NGPCA-constV', in contrast to NGPCA, which uses (3.2) for the competition.



Next: 3.2.3 Simulations
Up: 3.2 Extension of Neural
Previous: 3.2.1 Algorithm
Heiko Hoffmann
2005-03-22
![]() ). The error (3.2) depends on the size of the hyper-ellipsoid. Its volume is proportional to
V =
). The error (3.2) depends on the size of the hyper-ellipsoid. Its volume is proportional to
V = ![]()
![]() . For a big ellipsoid, (3.2) has therefore a huge bias, namely 2 ln V. Thus, if the other ellipsoids are much smaller, this huge ellipsoid often has a high rank, independent of the Euclidean distance of
. For a big ellipsoid, (3.2) has therefore a huge bias, namely 2 ln V. Thus, if the other ellipsoids are much smaller, this huge ellipsoid often has a high rank, independent of the Euclidean distance of ![]() to the center of the ellipsoid. Since the weight
to the center of the ellipsoid. Since the weight ![]() decreases exponentially with the rank,
decreases exponentially with the rank, ![]() is almost zero, and the ellipsoid cannot change its size anymore, it is `dead' (for example, figure 3.8.A). Thus, to avoid dead units, we tested an alternative error measure that is independent of the volume of the ellipsoid. This can be achieved by normalizing
is almost zero, and the ellipsoid cannot change its size anymore, it is `dead' (for example, figure 3.8.A). Thus, to avoid dead units, we tested an alternative error measure that is independent of the volume of the ellipsoid. This can be achieved by normalizing ![]() and
and ![]() such that the resulting volume
such that the resulting volume ![]() is one. Let
is one. Let
![]() and
and
![]() be the normalized values. They can be computed by
be the normalized values. They can be computed by